Why do we need Sampling?
Sampling is used when we try to draw a conclusion without knowing the population. Population refers to the complete collection of observations we want to study, and a sample is a subset of the target population. Here’s an example. A Gallup poll¹, conducted between July 15 to 31 last year, found that 42% of Americans approve of the way Donald Trump is handling his job as president. The results were based on telephone interviews of a random sample of ~4500 calls (assuming one adult per call. ~4500 adults), aged 18 and older, living in the U.S. The poll was conducted during a period of controversy over Trump’s social media comments. For this survey, the population is ALL the U.S citizens aged 18 and older, and the sample is 4500 adults.
If sampling is done wrong, it will lead to biases that affect the accuracy of your research/survey results. To avoid selection biases, we have to carefully choose a subset of a population that can be representative of the group as a whole.
Types of Probability Sampling
Simple Random Sampling

Simple random sampling means we randomly select samples from the population where every unit has the same probability of being selected.
Pros: there’s no need to divide the population into subgroups or take any other additional steps before selecting members of the population at random.
Cons: the samples might not be representative, and it could be time-consuming for large populations.
Use Case: it’s used when we don’t know too much about the population.
#let's create a dataframe first!
import numpy as np
import pandas as pd
from numpy.random import randn
# Define total number of customers
number_of_customers = 10
# Create data dictionary
data = {'customer_id':np.arange(1, number_of_customers+1).tolist(),
'customer_life_time_value':randn(10)}
# Transform dictionary into a data frame
df = pd.DataFrame(data)
# View data frame
df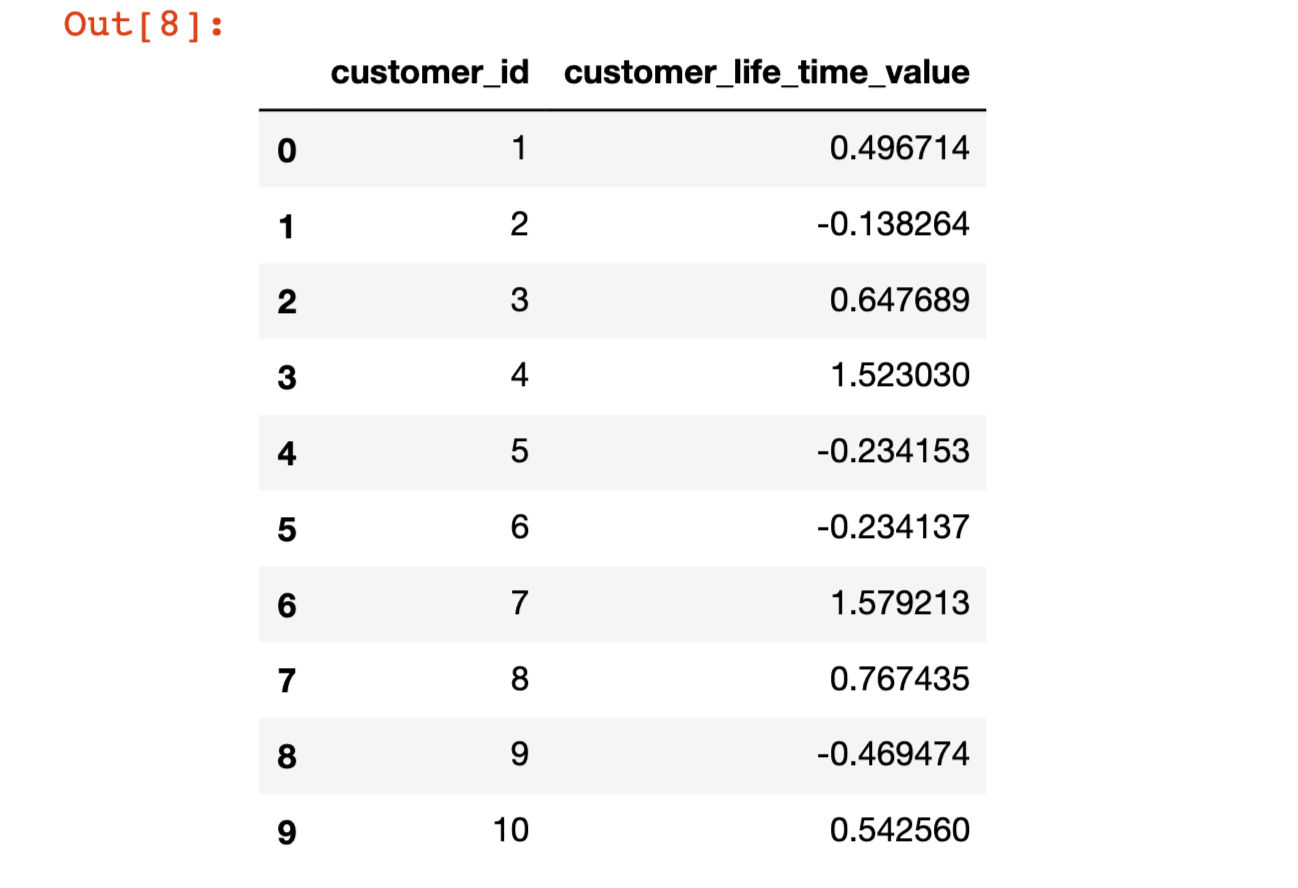
#only using random(), we can generate 4 samples from this dataset
# Obtain simple random samplesimple_random_sample = df.sample(n=4).sort_values(by='customer_id')
simple_random_sample

Stratified Sampling

For stratified sampling the population is divided into subgroups (called strata), then randomly select samples from each stratum.
Pros: it captures key population characteristics, so the sample is more representative of the population.
Cons: it’s ineffective if subgroups cannot be formed.
Use Case: it’s commonly used in geographic sampling where strata can be states, countries, or ecoregions.
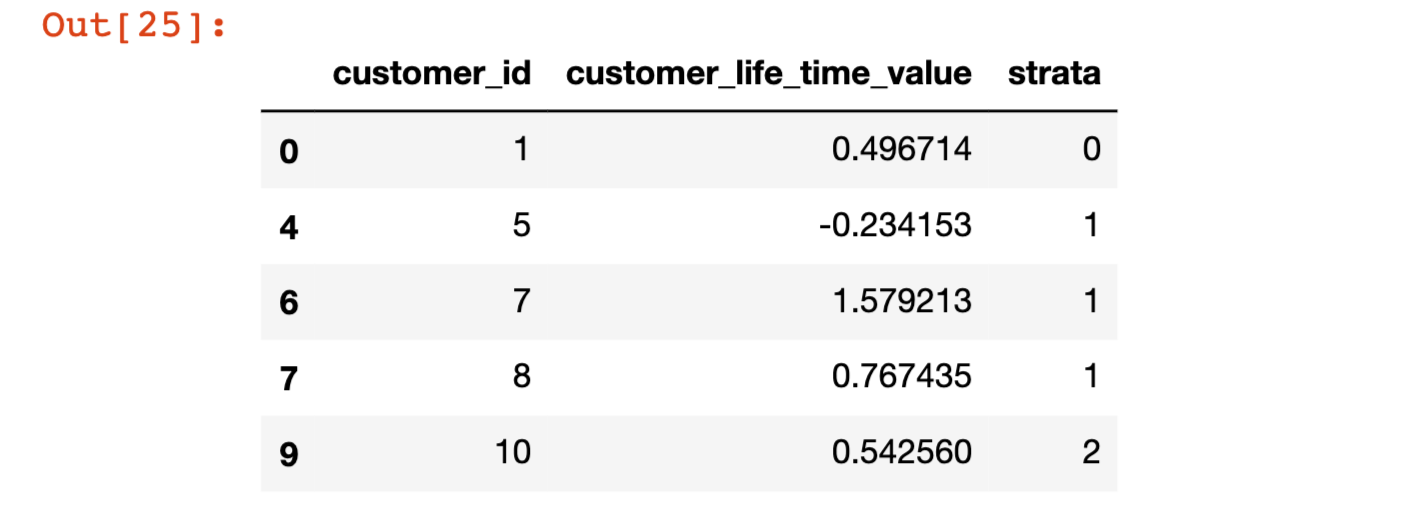
#Let's add subgroup labels to the datasetdf['strata']=[0, 0, 0, 1, 1, 1, 1, 1, 2, 2]sss = StratifiedShuffleSplit(n_splits=5, test_size=0.5, random_state=0)for x, y in sss.split(df, df['strata']):
stratified_random_sample = df.iloc[y].sort_values(by='customer_id')
stratified_random_sample
Cluster Sampling
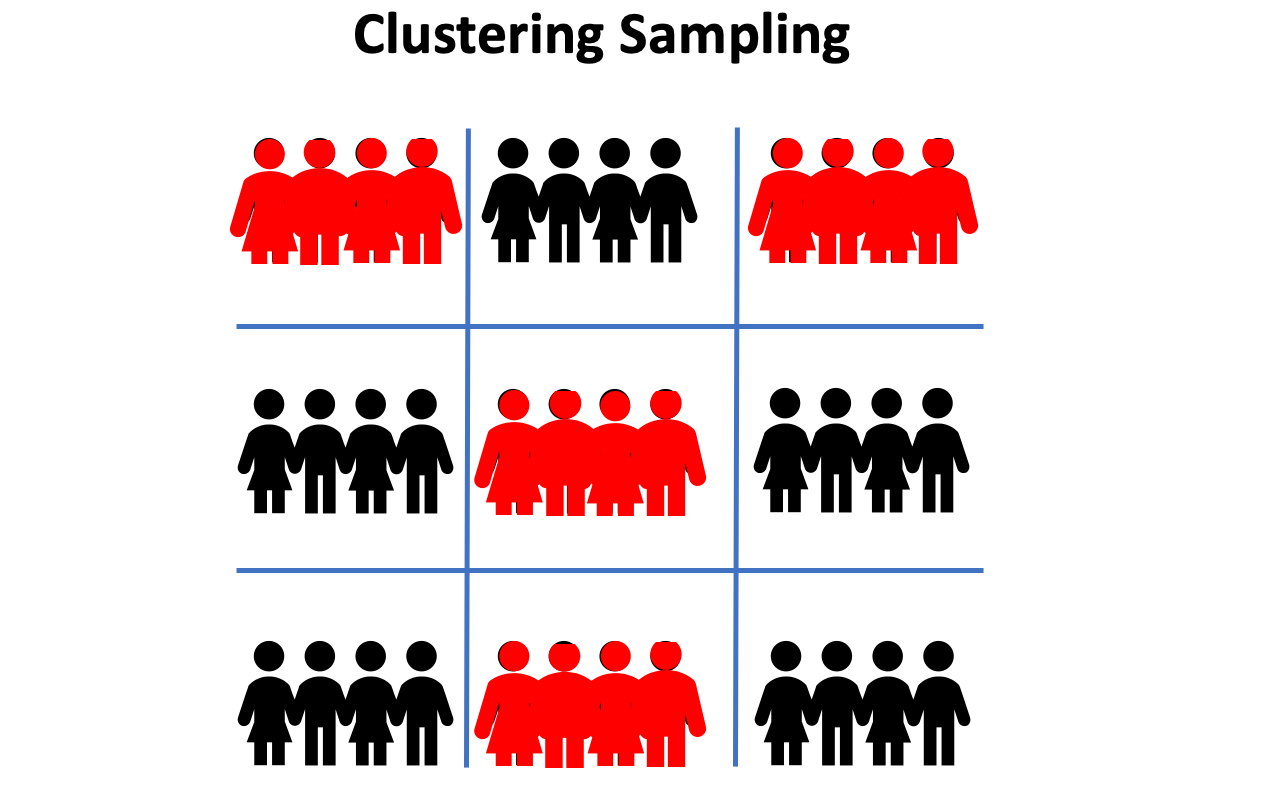
For clustering sampling, the population is divided into different clusters. Then a fixed number of clusters are randomly sampled and all units within each of the selected clusters are included in the sample.
Pros: it reduces variability, and it’s easy to conduct.
Cons: it is possible to introduce bias during sampling.
Use Case: it’s used when all individuals in each cluster can be representative of the populations.
#create 4 different clusters based on customers' lift time valuesdf['cluster'] = pd.cut(df['customer_life_time_value'], bins=4, labels=False) +1

# predefine which clusters/groups we want to select samples fromn=[2,4]def clustering_sampling(df,n):
df_list=[]
for i in range(len(n)):
df1=df[df['cluster']==n[i]]
df_list.append(df1)
final_df=pd.concat(df_list, ignore_index=True)
return final_dfclustering_sampling(df,n)

Systematic Sampling

A systematic sample is drawn by selecting units systematically from a sample frame. (i.e every other unit is included in the sample)
Pros: it can eliminate clustered selection, and it’s simple to execute.
Cons: we need to predetermine the estimated population size. It doesn’t work well if the population has a type of standardized pattern.
Use Case: it’s used when the relevant data does not exhibit patterns.
def systematic_sampling(df, step):
indexes = np.arange(0,len(df),step=step)
systematic_sample = df.iloc[indexes]
return systematic_sample
systematic_sampling(df, 1)










No comments:
Post a Comment